Where Do We Use Trigonometry?
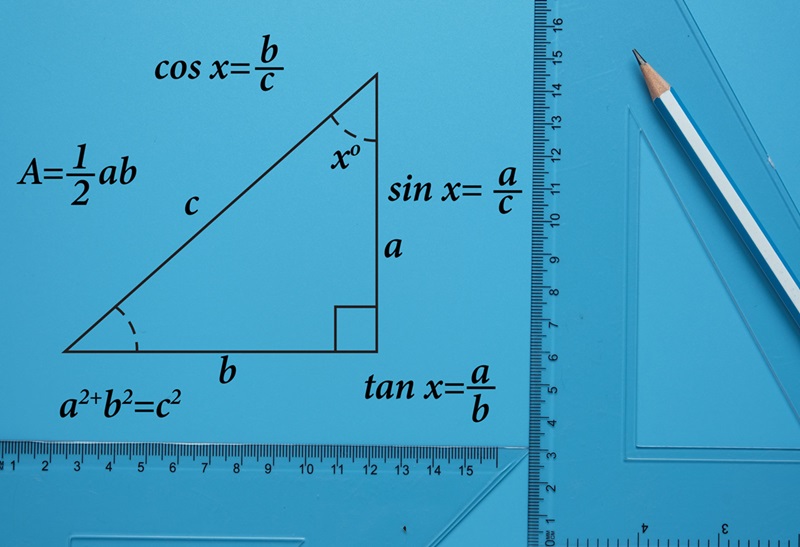
Trigonometry, a branch of mathematics that deals with the relationships between the angles and sides of triangles, is a versatile and essential tool used in various fields.
From engineering to physics, architecture to computer science, the applications of trigonometry are widespread and impactful.
In this comprehensive guide, we will delve into the practical applications of trigonometry and how it plays a crucial role in solving real-world problems.
Understanding The Basics
Before exploring the applications, it’s crucial to have a solid grasp of the fundamentals of trigonometry. At the heart of this mathematical discipline is the Unit Circle Chart, a powerful tool that aids in understanding trigonometric functions.
The Unit Circle Chart
The Circle Unit Chart is a circular chart with a radius of 1 unit, centered at the origin of a coordinate plane. It is a fundamental component in trigonometry, providing a visual representation of angles and their corresponding trigonometric values. This chart serves as a key reference for understanding sine (sin), cosine (cos), and tangent (tan) functions.
Sin, Cos, Tan Unit Circle Chart
The sin cos tan unit circle chart visually depicts the relationships between angles measured in radians and the corresponding values of sine, cosine, and tangent. This chart is instrumental in solving trigonometric equations and understanding the behavior of these functions.
Trigonometry Unit Circle Chart in Radians
In trigonometry, angles are often measured in radians, and the Unit Circle Chart is no exception. The unit circle chart in radians provides a precise way to express angular measurements, allowing for accurate calculations in trigonometric applications.
Unit Circle Chart Values
Understanding the values presented on the Unit Circle Chart is crucial for applying trigonometry in practical situations. Each point on the chart corresponds to a unique angle, and the coordinates of these points provide the sine, cosine, and tangent values for that angle.
Practical Applications of Trigonometry
Now that we have a solid foundation in the basics, let’s explore the diverse applications of trigonometry across various fields.
Engineering
Structural Analysis: Trigonometry is extensively used in engineering for structural analysis. Engineers employ trigonometric principles to calculate forces, stresses, and angles in various structures, ensuring their stability and safety.
Electrical Engineering: Trigonometry plays a pivotal role in analyzing alternating current (AC) circuits. Engineers use trigonometric functions to understand phase differences, impedance, and other critical parameters in electrical systems.
Physics
Projectile Motion: Trigonometry is employed to analyze and predict the trajectory of projectiles. Whether it’s a launched rocket or a basketball in motion, understanding angles and distances is essential for accurate predictions.
Wave Analysis: In the study of waves, trigonometric functions are used to model and analyze waveforms. This is crucial in fields like acoustics and optics, where wave behavior is a central focus.
Architecture
Building Design: Architects use trigonometry to calculate angles, dimensions, and proportions in building design. This ensures that structures are aesthetically pleasing, functional, and structurally sound.
Surveying: Trigonometry is indispensable in land surveying. Surveyors use trigonometric principles to measure distances and angles accurately, creating precise maps and property boundaries.
Computer Science
Computer Graphics: Trigonometry is the backbone of computer graphics. Algorithms for rendering images, creating animations, and determining 3D object positions heavily rely on trigonometric functions.
Animation and Game Development: In animation and game development, trigonometry is used to model realistic movements, simulate physics, and create immersive virtual environments.
What Is The Trig Circle Chart, And How Is It Used In Trigonometry?
The Trig Circle Chart, also known as the Unit Circle Chart, is a circular diagram used in trigonometry to visualize the relationships between angles and trigonometric functions such as sine, cosine, and tangent.
Why Are Angles In Trigonometry Often Measured In Radians On The Unit Circle Chart?
Radians provide a more natural and consistent way to measure angles on the Unit Circle Chart. Using radians simplifies calculations and maintains a direct correlation between arc length and angle measure.
How Does Trigonometry Contribute To Structural Analysis In Engineering?
Trigonometry is crucial in structural analysis as it helps engineers calculate forces, stresses, and angles within structures. This ensures the stability and safety of buildings, bridges, and other engineering projects.
How Is Trigonometry Applied In Computer Graphics And Game Development?
In computer graphics and game development, trigonometry is used to model realistic movements, simulate physics, and calculate positions of 3D objects. Algorithms for rendering images and creating immersive virtual environments heavily rely on trigonometric functions.
Conclusion
Trigonometry is not just a mathematical concept learned in classrooms; it is a powerful tool with practical applications across a multitude of fields. Whether you are an engineer designing a structure, a physicist studying wave behavior, or a computer scientist creating virtual worlds, a solid understanding of trigonometry and the Unit Circle Chart is essential. As we celebrate the versatility and significance of trigonometry on its one-year birthday, it’s clear that its impact will continue to shape the way we solve real-world problems for years to come.